Astrophysics
Schwarzschild black hole
This step took a working simulation and made it admissions-ready: coherent visuals, clean defaults, sensible sliders, and copy that helps a non-specialist understand what they’re seeing. I locked physics choices from prior steps, removed “debug” overlays from the public view, and tuned color, contrast, and typography so the viewer’s eye lands on the physics, not the UI.
Why this problem?
A strong project can still stumble if the first five seconds confuse the audience. Final polish isn’t cosmetics—it’s accessibility. The goal here was a version any curious reader can explore without me in the room.
Problem Statement
How do I present the simulation so it’s clear, fast, and honest to the math—while keeping interaction playful and safe (no sliders that break the scene, no colors that mislead the interpretation)?
Collaborating with people (discord)
I ran a “five-minute test”: friends and a couple of Discord folks got a link and no instructions. I noted where they hesitated, what they tried first, and which labels they misread. That pass surfaced micro-frictions (ambiguous units, cryptic variable names) I couldn’t see on my own.
Reflections
Polish forced me to defend every knob and caption. If I couldn’t explain it in a sentence, it didn’t ship. That constraint made the whole project tighter.
Blackhole Iterations
Step 1 was a sandbox. I wanted a fast way to test curve evolution on a 2D plane inside Desmos, so I wired a first-order ODE 𝑑𝑦/𝑑𝑥=𝑓(𝑥,𝑦) to a classic Runge–Kutta (RK4) loop and sprayed trajectories from randomized starting points. The goal wasn’t physical accuracy; it was to validate the numerics, step-size behavior, and visualization pattern I’d later reuse for real geodesics. Once this was stable and predictable, I had the scaffold to build the rest.
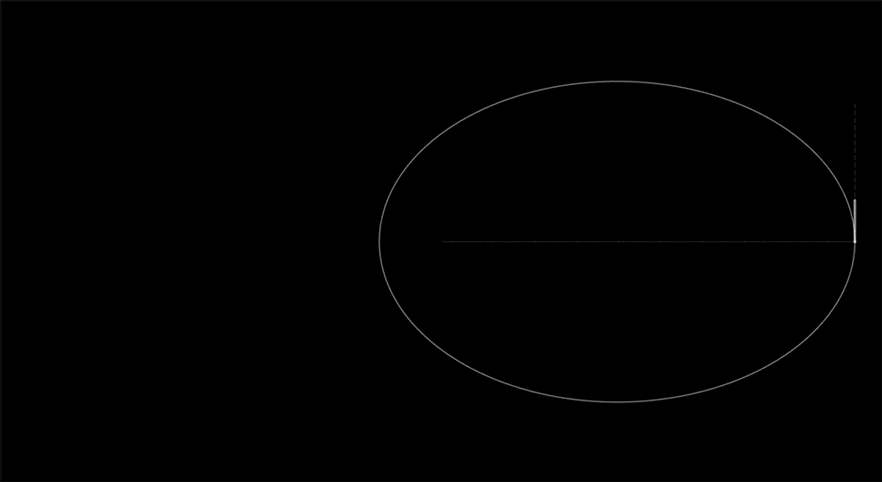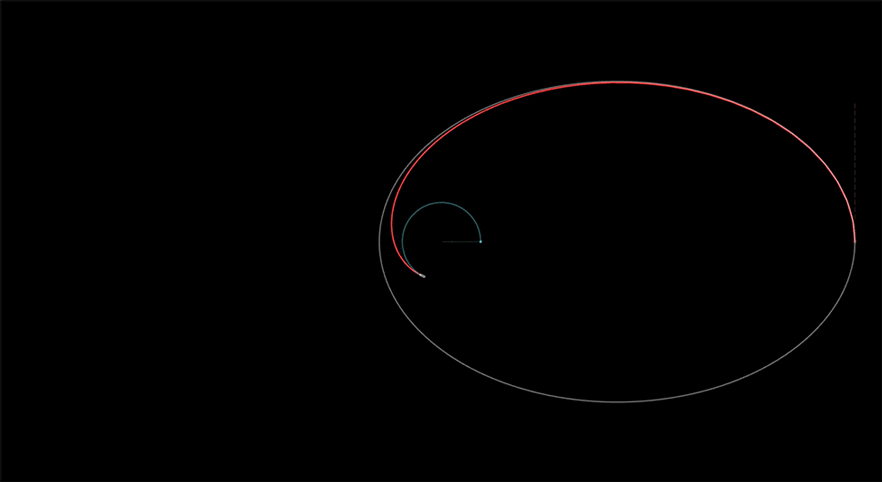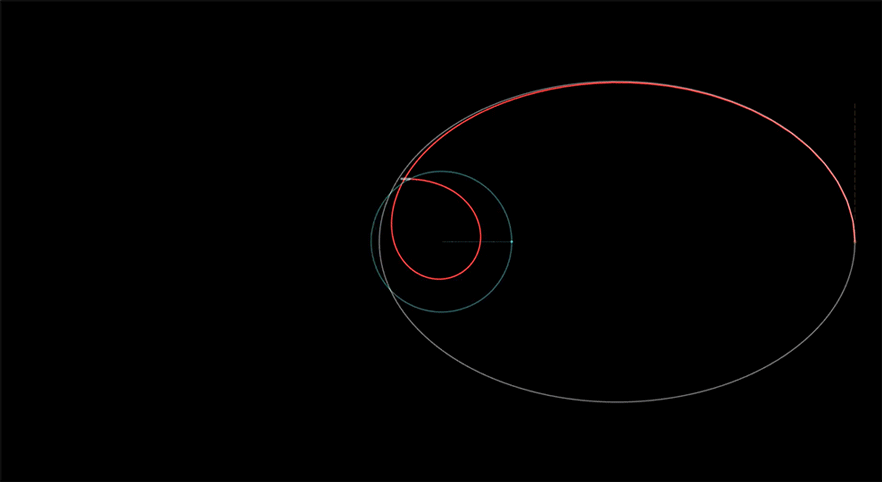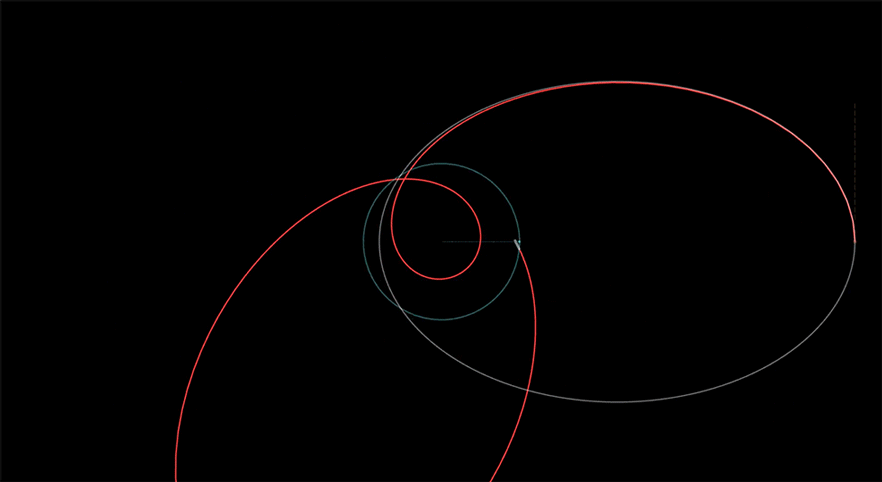
Version 1 - 2d Schwarzschild geodesics
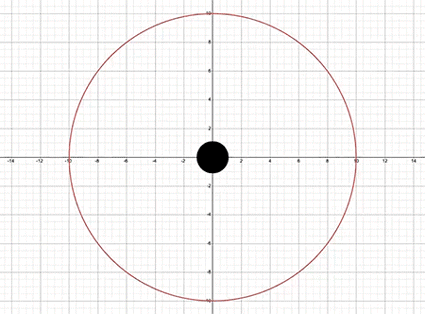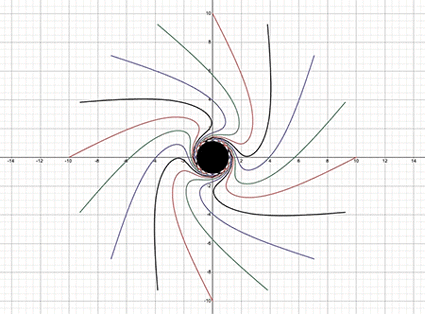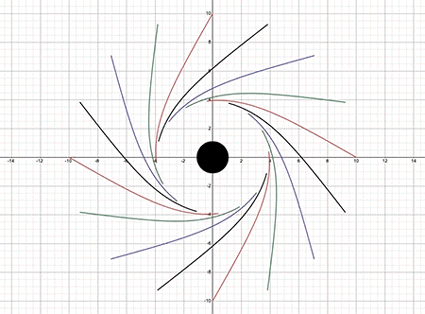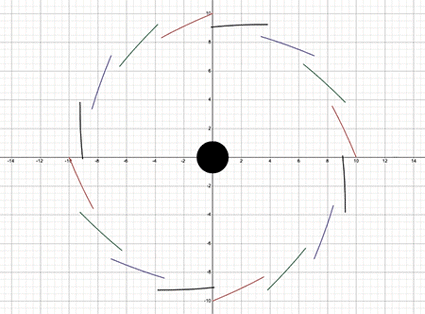
I wanted to see something move—a first, credible orbiting path in a black-hole spacetime—so I started simple: the equatorial plane of a Schwarzschild black hole. I built an interactive Desmos model that integrates the basic orbit-shape equation with Velocity Verlet, marks the photon sphere (1.5 𝑟𝑆) and ISCO (3 𝑟𝑆), and shades concentric bands using a simple gravitational potential factor to make the geometry feel physical. No lensing yet—just motion and structure I could trust.
Version 3 - Star gravitational lensing
I replaced the random point cloud with clean parametric “stars,” focused on crisp Einstein rings, and cut the lag from my earlier RK4 pass by simplifying the pipeline.
Version 5 - Null geodesics
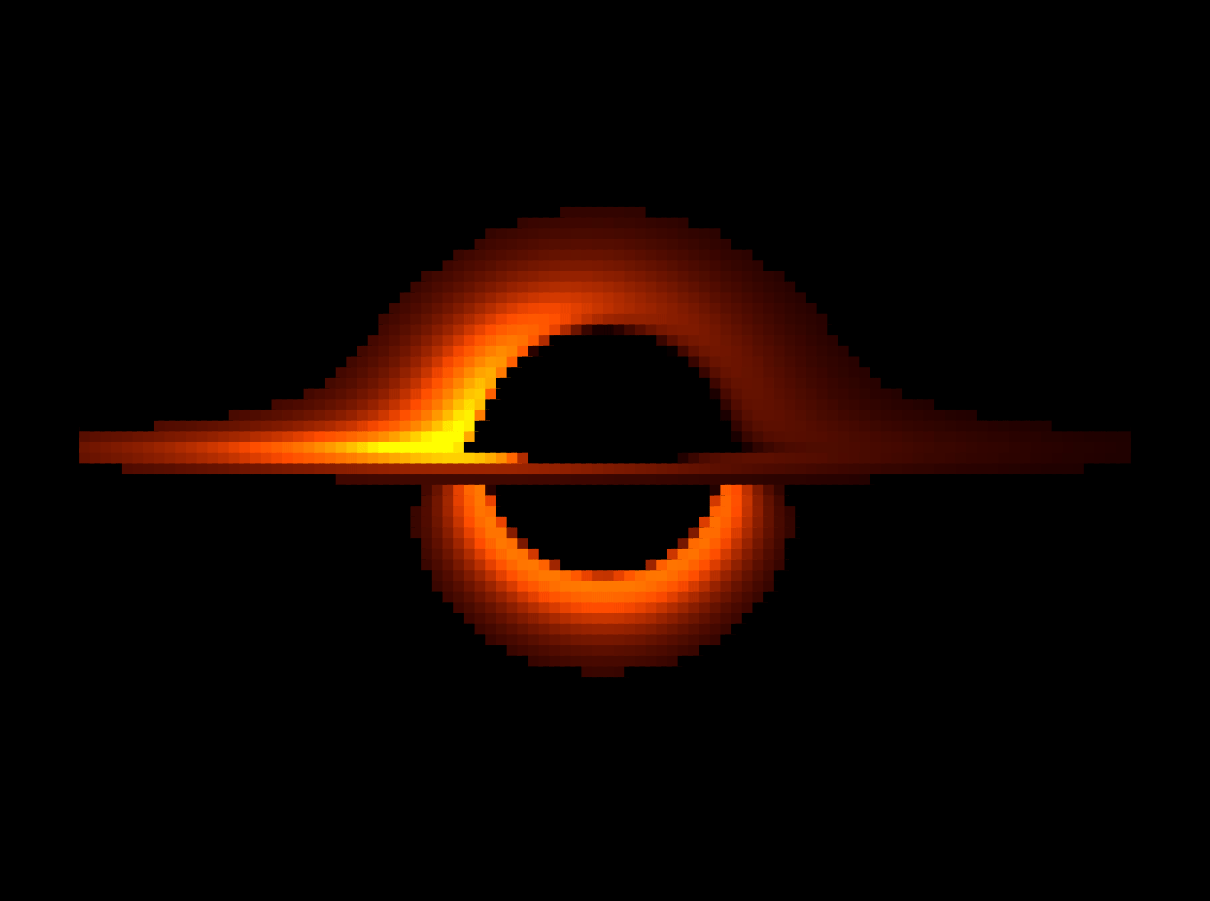
I replaced the “looks-right” warp with a real, equatorial Schwarzschild model. Instead of pushing pixels through a handmade distortion, I traced how light from a thin, emissive disk would be seen by a distant observer using the actual orbit-shape equations. The picture finally started behaving like a black-hole scene for physical reasons, not artistic ones.
Version 7 - 2d disk mapping
This step is where I stopped “eyeballing” and started treating the simulation like a small research note. I gathered the core references, organized the equations for equatorial Schwarzschild geodesics, and wrote a clean derivation-and-checks document. The goal wasn’t just to make pretty frames; it was to show exactly which formulas drive them and how I verified each choice.
Version 9 - Final product
This step took a working simulation and made it admissions-ready: coherent visuals, clean defaults, sensible sliders, and copy that helps a non-specialist understand what they’re seeing. I locked physics choices from prior steps, removed “debug” overlays from the public view, and tuned color, contrast, and typography so the viewer’s eye lands on the physics, not the UI.
Version 2 - Lensing proof of concept
I built a quick, visually convincing lensing sketch in Desmos by inventing a 2D “warper” around a putative black hole. The goal wasn’t physical accuracy yet; it was to see whether rings, arcs, and central dimming could appear on screen at all.
Version 4 - Approximate accretion disk lensing
I tested whether an optically thin accretion disk—painted on the equatorial plane and then mapped into the image—could produce a scene that “reads” like a black hole: a central shadow, a bright rim, and a skewed disk. This was still a prototype, but it let me move from dots and rings to a continuous texture that feels like a real astrophysical object.
Version 6 - proof of concept 3d Black hole
Desmos had finally come out with a shader, where I could color each point based on some function of x and y. I started experimenting with it to see if it was feasible for black hole simulation.
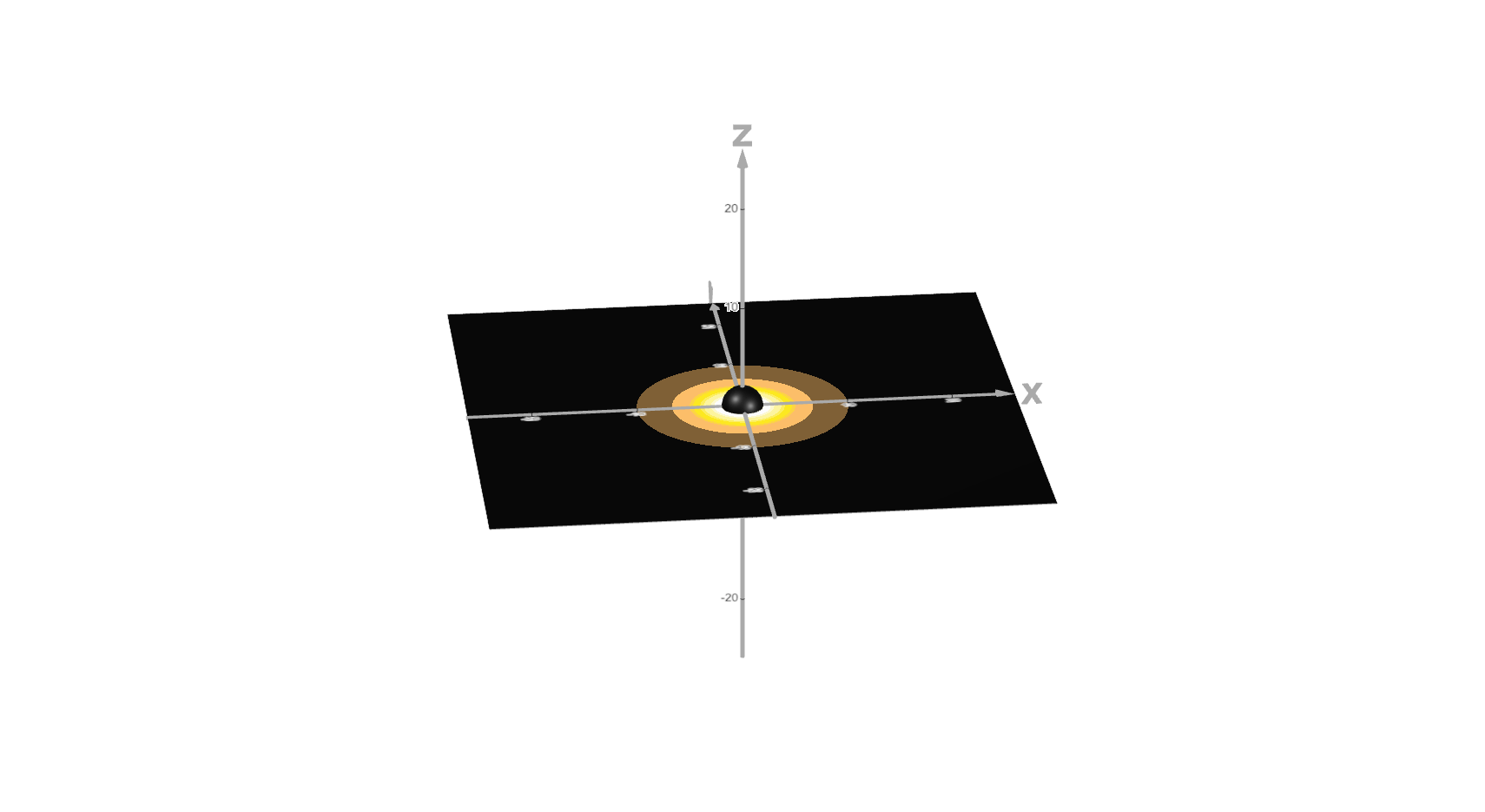
Version 8 - 3d disk mapping shader
This is where all the pieces finally talked to each other. I merged the equatorial-Schwarzschild geometry from earlier steps with the Doppler/gravity coloring, then added an image-processing pass to make frames both readable and honest to the physics I’d encoded. I treated this step like a “wind-tunnel”: integrate, stress-test, smooth the rough edges, and verify the outputs against quick analytic checks before committing to a final build.